kikuta | Basic Materials Group

物理量で、温度や密度などは物質の向きに関係しておらず、 $a$ 軸方向の温度だとか、ある特別な方向の密度というのは意味がありません。このような向きを考慮しない物理量をスカラー（scalar）といい、一つの数値で表せます。スカラーは0階（zero rank）のテンソル（tensor）とも呼ばれます。

スカラーに対して異なるタイプの物理量をベクトル（vector）といいます。ベクトルはスカラーと異なり物質の向きを常に気にします。例えば、力を物質に加える際には、どの向きにどのくらいの大きさでという、方向と大きさの情報が必要になってきます。他には、物質中のある点での電場(電界強度)、双極子モーメントやある点での温度勾配などがベクトルとして挙げられます。ベクトルを記号(変数)で表すときには $\boldsymbol E$ のように太字で表します。ノートに書く場合には、 $\mathbb E$ のように二重線文字にしたり、 $\vec{E}$ のように記号の上に矢印を書いたりします。ベクトルには方向と大きさが必要ですので、表現するのに２種類の数値が必要です。２種類の数値を方向と大きさとして表現する場合（方位・仰俯角と距離）もありますが、通常は、大きさを向きが分かるように空間成分に分けて表現します。まず、直交する３つの軸を決めて、それらを $x_1$ 軸、 $x_2$ 軸、 $x_3$ 軸（ $X$ 軸、 $Y$ 軸、 $Z$ 軸などでも良い）とします。これらの軸に沿うベクトルの成分を決めるのです。成分は単にベクトルのこれらの軸への射影です。 $x_1$ 軸方向の成分が $a_1$ 、 $x_2$ 軸方向の成分が $a_2$ 、 $x_3$ 軸方向の成分が $a_3$ だとすると、その大きさは $\sqrt{a_1^2+b_2^2+a_3^2}$ で与えられます。方向は、原点と原点から $x_1$ 軸方向に $a_1$ 進んで、続いて $x_2$ 軸方向に $a_2$ 進み、 $x_3$ 軸方向に $a_3$ 進んだ地点とを結ぶ直線の方向です。電場 $\boldsymbol E$ の $x_i$ 軸方向成分が $E_i$ （ $x_1$ 軸方向成分が $E_1$ 、 $x_2$ 軸方向成分が $E_2$ 、 $x_3$ 軸方向成分が $E_3$ ）のとき、ベクトル $\boldsymbol E$ は、

${\boldsymbol E} = E_i = \left( \begin{array}{c} E_1 \\ E_2 \\ E_3 \\ \end{array} \right)$

と書かれます。ベクトルはその成分を表す添字が１つであり、1階（1st rank）のテンソルとも呼ばれます。

ベクトルの考え方を拡張したものがテンソルです。例えば、電圧 $V$ を電気伝導体材料に印加して電流 $I$ が流れたとします。このとき材料の電気抵抗を R とすると、

$I = \frac{1}{R} V$

です。つまり、オームの法則（ohm’s law）です。ここで、電圧がどの向きに印加されて、電流がどの向きに流れたのかも意識して書くことにします。加えて、材料のサイズによらずに式を書くために、電圧を電場 $\boldsymbol E$ に、電流を電流密度 $\boldsymbol j$ と書くことにします。そうすると、オームの法則は、

${ \boldsymbol j } = \sigma { \boldsymbol E }$

と書くことができます。ここで、 $\sigma$ は電気伝導率を表します。各成分について書きなおせば、

$j_1 = \sigma E_1, \ \ j_2 = \sigma E_2, \ \ j_3 = \sigma E_3$

と電流密度の成分は電場の相当する成分に比例しますので、電流は電場と同じ向きに流れます。さらに、材料のどの方向に電場を加えても流れる電流密度は一緒です。しかし、材料に異方性がある場合、電場を印加する方向によって流れる電流密度が異なります。この場合に上式は、

$\begin{eqnarray*}j_1 &=& \sigma_{11} E_1 + \sigma_{12} E_2 + \sigma_{13} E_3 \\j_2 &=& \sigma_{21} E_1 + \sigma_{22} E_2 + \sigma_{23} E_3 \\j_3 &=& \sigma_{31} E_1 + \sigma_{32} E_2 + \sigma_{33} E_3 \\\end{eqnarray*}$

と書けます。ここで、 $\sigma_{ij}$ は電気伝導率の成分を表します。電流密度の成分は電場の全ての成分と関連していることになり、一般的に電流は電場と同じ向きには流れません。例えば、電場を $x_1$ 軸方向に印加した（ $E_1 \ne 0, E_2 = E_3 = 0$ ）とき、電流密度 $\boldsymbol j$ は、

$j_1 = \sigma_{11} E_1, \ \ j_2 = \sigma_{21} E_1 \ \ j_3 = \sigma_{31} E_1$

となります。 $x_1$ 軸方向に電流 $j_1$ が流れるほかに、 $\sigma_{21}$ や $\sigma_{31}$ のために、 $x_2$ 軸方向や $x_3$ 軸方向にも電流が流れることを意味します。

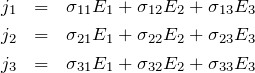
異方性のある材料の電気伝導率を表現するために、電気伝導率を

$\sigma_{ij} = \left( \begin{array}{ccc}\sigma_{11} & \sigma_{12} & \sigma_{13} \\\sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \\ \end{array} \right)$