誘電率 ![]() は、物質に電場
は、物質に電場 ![]() を印加した時にどのくらい分極
を印加した時にどのくらい分極 ![]() するかを表す量ですが、電束密度
するかを表す量ですが、電束密度 ![]() との関係で、
との関係で、
![]()
ここで、 ![]() は電気感受率で、
は電気感受率で、
![]()
![]()
物質に電場を印加すると分極が生じます。分極の起源には様々なものがありますが、いずれにしても、 物質に電場が印加されて分極が現れて安定状態になるまでには時間がかかるのです。式の上では、 電場 ![]() に対して分極
に対して分極 ![]() の応答が遅れます。 分極
の応答が遅れます。 分極 ![]() が遅れるってことは、電束密度
が遅れるってことは、電束密度 ![]() も遅れます。いまは誘電率
も遅れます。いまは誘電率 ![]() を気にしたいので、電場
を気にしたいので、電場 ![]() と電束密度
と電束密度 ![]() の時間的ずれだけに着目します。簡単のため、電場を
の時間的ずれだけに着目します。簡単のため、電場を ![]() 、電束密度を
、電束密度を ![]() として、電束密度が
として、電束密度が ![]() だけ電場よりも遅れるとします。電束密度の式を変形して電場で表せるようにすると、
だけ電場よりも遅れるとします。電束密度の式を変形して電場で表せるようにすると、
(1) 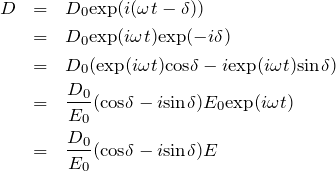
![]()
![]()
![]()
この遅れによって、どれだけの電気エネルギーが使われるのかを計算します。単位体積当たりの電力 ![]() を1周期分積分して周期
を1周期分積分して周期![]() で割ります。 単位体積当たりの電力
で割ります。 単位体積当たりの電力 ![]() は電流密度
は電流密度 ![]() と電場
と電場 ![]() の積であり、電流は電荷の時間微分なので、電束密度
の積であり、電流は電荷の時間微分なので、電束密度 ![]() の時間微分は電流密度
の時間微分は電流密度 ![]() に相当します。
に相当します。
(2) 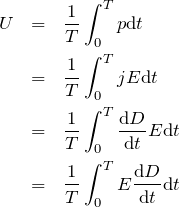
ここで、 電場
(3) 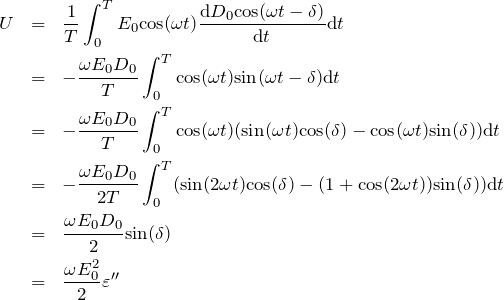
となり、これだけエネルギーを消費していることになります。 遅れ
導電性がある物質に電場を加えたとき、ジュール熱としてどれだけエネルギーを消費するのかは、![]() を導電率として、
を導電率として、
(4) 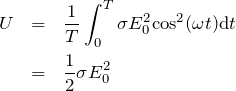
で与えられますので、先ほどの誘電損失と比較して、
![]()
という関係式が得られます。複素誘電率の虚数部は試料の導電率に相当する量(角周波数で割りますけど)を表していることが分かります。
誘電率と比誘電率は異なるものですが、https://www.jstage.jst.go.jp/article/jceeek/2020/0/2020_247/_pdf/-char/jaなどの論文で使われる複素比誘電率と複素誘電率は異なったものでしょうか?
直接、論文を書いたところへ問い合わせるべきとは思います。ざっと読んだところ、論文というかアブストラクトだとおもいますが、登場するのは、複素比誘電率だけで、これのことを誘電率、比誘電率などと呼んでいるようです。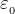 」に比べて何倍かということなので、たいてい1以上の値で表現されます。また複素数というのは、試料が電気的には純粋なコンデンサ
」に比べて何倍かということなので、たいてい1以上の値で表現されます。また複素数というのは、試料が電気的には純粋なコンデンサ 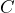 だけで構成されているのではなく、並列に導電性の成分
だけで構成されているのではなく、並列に導電性の成分 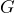 (抵抗の逆数)がある、試料が
(抵抗の逆数)がある、試料が 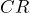 の並列回路だとして考えたものです。このときの
の並列回路だとして考えたものです。このときの 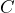 に対応する誘電率が複素(比)誘電率の実数部で、虚数部はGに対応する量を表します。したがって、複素(比)誘電率の虚部が
に対応する誘電率が複素(比)誘電率の実数部で、虚数部はGに対応する量を表します。したがって、複素(比)誘電率の虚部が 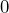 であれば、試料が全く損失の無い純粋なコンデンサに見えるということです。
であれば、試料が全く損失の無い純粋なコンデンサに見えるということです。
比誘電率は、「真空の誘電率
材料Aと材料BのコンポジットCの誘電特性は、材料A、Bの誘電率ε’A、ε’B、誘電損率ε”A、ε”B及び、材料A、Bの体積分率VA、VBを用いて以下のような計算式での算出は妥当でしょうか?
ε’A×VA+ε’B×VB=ε’C
ε”A×VA+ε”B×VB=ε”C
ε”C/ε’C=tanδC
材料が複数になると途端に難しくなります。以下では並行平板コンデンサをイメージします。
簡単には、電極と平行に層状に材料が積み重なった(塗布された)場合には、それぞれの材料のコンデンサが直列につながったと見做せるので、有効誘電率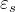 は、
は、
であり、電極と垂直であれば、それぞれの材料のコンデンサが並列につながったと見做せるので、有効誘電率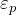 は、
は、
と表せます。ご質問の式だと、この後者のモデルに当てはまります。
いずれも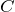 は要らないですが。
は要らないですが。実際には、母材となる誘電体に少量の添加物を混ぜたり、複数の粉末材料を混ぜて固めたものだったり、するので、以上に挙げた二つの誘電率の中間となることが予想されます。また、添加物が母材の中で互いにくっついているかどうかや添加物の表面や焼結体の界面などが、材料内部の誘電率と異なる場合には、電場が一様ではなくなるので、更なる考察が必要になります。
母材の中に少量の添加物がある場合には、Maxwell-Garnet 則というのが良く用いられます。カシオ計算機の計算サイトに載っていますので、数値を代入するだけで有効誘電率を求めることができます。母材の方の誘電率を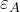 とすれば、
とすれば、
というような式になります。
その他、有効媒質近似(Effective Medium Approximations)という名前で多くのモデルが提案されています。中でも Bruggeman のモデルが 、Maxwell-Garnet 則 の表現よりも混合率が高くなる時に、良く用いられます。
この式から、 を求めます。巨視的に眺めたときに分極が生じないように考えると出てくるような気がします。?
を求めます。巨視的に眺めたときに分極が生じないように考えると出てくるような気がします。?
さらに、材料の粒径が分布しているとか複雑になると、数値計算で、ああでないか、こうでないか、というのが多数提案されています。
実際に複合材料を取り扱ったことがないので、表面的な回答ですみません。
早速、ご回答いただきありがとうございます。
母材A中に別の材料Bが分散している系を考えていますので、混合率により考えるモデルが異なる、ということですね。
このようなモデル式は誘電率ε’だけでなく、誘電損率ε”にも適用できるのでしょうか?
はい、上記の式は誘電率 が複素誘電率
が複素誘電率 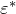 だとしても、成り立ちますので、
だとしても、成り立ちますので、
として、誘電率の実部と虚部を計算できます。※ 虚数単位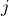 の前の符号がマイナスであることに注意してください。
の前の符号がマイナスであることに注意してください。
導電体の場合には、誘電率 の代わりに電気伝導度
の代わりに電気伝導度  に置き換えることで同じことが言えるはずです。
に置き換えることで同じことが言えるはずです。
ご回答ありがとうございます。
例えばMaxwell-Garnet則が適用できる場合、式中のεA、εBのところを各材料の複素誘電率の実部ε’A、ε’Bあるいは虚部ε”A、ε”Bに置き換えて計算することで、複合体の実部ε’MGと虚部ε”MGをそれぞれ算出し、ε”MG/ε’MGから複合体の誘電正接tanδMGを算出できる、ということですね。
誘電率 が複素誘電率
が複素誘電率 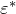 だとして置き換えますので、
だとして置き換えますので、
としますので、計算はかなり厄介です。
計算が合っているかどうかわかりませんが、
な感じかと。
ああ、せっかく計算したのに、表示されないかも。
はじめは電場をE0exp(iwt)と複素数で表示していたのに、エネルギー計算の部分からE0cos(wt)と変えられるのはなぜですか。
複素数で表していたときの虚部の情報はどこに行ってしまったのでしょうか。
回答よろしくお願いします。
なかなか痛いところを突かれました。何か教科書的なものを見ながら書いたわけではないので、そもそも式が正しいかどうかに不安はあるものの、大体は合っていると思います。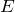 や電束密度
や電束密度 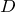 の虚部は(ある時刻での)位相を表すのに使っていましたが、1周期分のエネルギーにはある時刻でという概念はありませんので。なんか、消化不良な回答ですみません。
の虚部は(ある時刻での)位相を表すのに使っていましたが、1周期分のエネルギーにはある時刻でという概念はありませんので。なんか、消化不良な回答ですみません。
回答としては、1周期分で消費されるエネルギーだけを計算するためです。電場
what is the relationship between dielectric constant and electric flux density response? how do you get a formula like that?
The first formula written in this page is relation between an electric field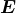 and an electric flux density
and an electric flux density 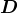 (or electric displacement).
(or electric displacement). is a measure of the electric polarizability of a dielectric material. The electric displacement field
is a measure of the electric polarizability of a dielectric material. The electric displacement field 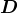 resulting from an applied electric field
resulting from an applied electric field 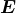 is,
is,
The permittivity
. is often represented by the relative permittivity
is often represented by the relative permittivity 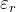 which is the ratio of the absolute permittivity
which is the ratio of the absolute permittivity  and the vacuum permittivity
and the vacuum permittivity 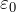 ,
,
The permittivity
.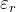 is directly related to electric susceptibility
is directly related to electric susceptibility 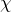 of the material by,
of the material by,
The relative permittivity
.
So, the relation,
holds.
The susceptibility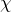 is usually defined as the constant of proportionality (which may be a tensor) relating an electric field
is usually defined as the constant of proportionality (which may be a tensor) relating an electric field 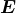 to the induced dielectric polarization density
to the induced dielectric polarization density 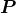 that,
that,
.
誘電率εと複素誘電率ε*を関係付ける式はあるのでしょうか?
複素誘電率の実部が誘電率に等しいとしたε’=εか、複素誘電率の絶対値が誘電率に等しいとした|ε*|=(ε’^2+ε”^2)^(1/2) のどちらかが成立するのではないかと考えています。
誘電率 をどのようにして測定したのかに依存します。
をどのようにして測定したのかに依存します。
例えば、損失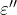 のあるコンデンサを損失が無いものとして測定した誘電率
のあるコンデンサを損失が無いものとして測定した誘電率  は、損失の分も容量だとして扱われるので、
は、損失の分も容量だとして扱われるので、
になります。コンデンサに交流電源(角振動数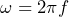 )をつないで電流を測定して、コンデンサにかかる電圧(振幅)
)をつないで電流を測定して、コンデンサにかかる電圧(振幅)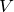 を流れる電流(振幅)
を流れる電流(振幅)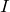 で割ると、インピーダンスの大きさ
で割ると、インピーダンスの大きさ 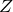 が分かりますので、
が分かりますので、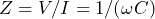 と した静電容量
と した静電容量 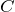 は、本当の純粋な静電容量
は、本当の純粋な静電容量 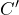 とコンデンサに並列な抵抗(損失の分)
とコンデンサに並列な抵抗(損失の分)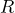 があると考えると、
があると考えると、
となるので、損失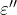 に関係する
に関係する 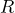 の分だけ、静電容量が大きめに測定されてしまいます。
の分だけ、静電容量が大きめに測定されてしまいます。
静的にコンデンサの容量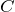 を測るのであれば、直流電源を既知の抵抗
を測るのであれば、直流電源を既知の抵抗  を介してコンデンサに繋ぎ、流れる電流の時間変化を測定すれば、電流の減衰曲線の時定数
を介してコンデンサに繋ぎ、流れる電流の時間変化を測定すれば、電流の減衰曲線の時定数 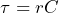 から静電容量
から静電容量 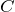 を求めることができ、そこから誘電率
を求めることができ、そこから誘電率  を求めることができます。このときの誘電率
を求めることができます。このときの誘電率  には損失が含まれていませんので、
には損失が含まれていませんので、 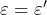 です。
です。