辞書的な定義で結晶は、「原子が規則正しく配列している固体。積み重なり行われた事柄が、一つの形で現れること。」などと書かれます。結晶は英語で crystal なのでクリスタルと片仮名で表記されることも多いのですが、クリスタルというと水晶やクリスタルグラスを差すことが多いようで、電気回路では水晶発振子です。なお、水晶は結晶ですが、クリスタルグラスはガラス（非晶質）であり結晶ではありません。また、英語で「汗と涙の結晶」の意味での結晶は、fruit （果実）でしょうか。
物質は大きく分けて、三態（さんたい）または三相（さんそう）と呼ばれる、固体（固相）、液体（液相）、気体（気相）の状態に分けられます。固体は、原子、分子、イオンなどの粒子が集まって粒子が振動する以外は自由に動けない状態といわれますが、全く動かないわけではありません。応力を加えると変形したり、電気を加えると分極するのは、原子や分子がある程度動いているからなのです。結晶はすべて固体ですがすべての固体が結晶ではなく、結晶以外に非晶質と呼ばれるガラスあるいはアモルファスがあります。
結晶は原子が規則正しく配列しているので、その規則性を用いて分類されます。２種類の原子（AとB）を直線状に配列させると、
- ABABABABABAB…
- ABBABBABBABB…
- AABBAABBAABB…
- ABBAABBAABBA…
などの並べ方を考えることができます。初めのものは AB の並びが繰り返されるという規則があり、２番目は ABB が、３番目と４番目は AABB が繰り返されています。原子の数が増えると繰り返しの単位にいくつかのバリエーションが生まれます。２番目では、ABB の代わりに BBA や BAB を考えることができますし、３番目では、ABBA や BBAA、BAAB が思いつきます。以上のような並びには周期性があります。近年、
- ABAABABAABAABABAABABAABAABABAABAAB…
- ABABAABABAABABABAABABAABABABAABABA…
のような周期性のない並び方が議論になりました。初めのものは、Aを親、Bを子と見てください。
- A (最初に親がいます。)
- AB (1.の親Aが子Bを産みました。)
- AB A (2.の親Aが子Bを産み、子Bが親Aになりました。)
- AB A AB (以後、A⇒AB、B⇒A を繰り返します。)
- ABAABABA
- ABAABABAABAAB
- ABAABABAABAABABAABABA
- ABAABABAABAABABAABABAABAABABAABAAB
下の例では、1から20までの整数を考えこれをAとします。また、20までの2の平方根1.41421356… の整数倍を考えてBとします。これらを数の小さいものから順にならべて得られます。これら二つの例には、繰り返しの単位がなく周期性が見られませんが、並び方の規則性は存在します。このような配列を原子や分子が持つ固体を準結晶といいます。準結晶は急冷した合金に見られることがあります。
準結晶以外の典型的な結晶は、その配列の形から分類され、１次元結晶では周期 
だけしか存在しませんので１種類の形の格子しかありません。鏡映の対称性を考慮すると2種類の結晶点群と2種類の空間群に分類されます。２次元結晶では周期 
と面上での軸の交差角度 
が配列の形を決めるので、
- 斜交、斜方、平行四辺形 (Oblique)
- 長方形 (Rectangular)
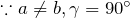
- 正方形 (Square)
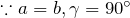
- 六方、三方、三角 (Hexagonal)
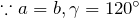
の４種類の格子に分類されます。また、並進対称性を考慮すると5種類のブラベー格子に分類され、回転と鏡映の対称性を考慮すると10種類の結晶点群、並進と映進の対称性も考慮すると17種類の空間群に分類されます。３次元結晶では、
- 三斜 (Triclinic)
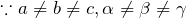
- 単斜 (Monoclinic)
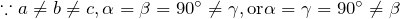
- 斜方、直方 (Orthorhombic)
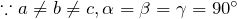
- 正方 (Tetragonal)
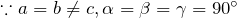
- 立方、等軸 (Cubic)
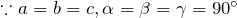
- 三方、菱面体 (Trigonal)
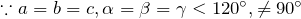
- 六方 (Hexagonal)
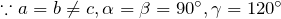
の7種類の格子（結晶系）に分類されます。また、並進対称性を考慮すると14種類のブラベー格子に、回転と鏡映、反転、回反の対称性を考慮すると32種類の結晶点群、並進、映進、らせんの対称性を考慮すると230種類の空間群に分類されます。